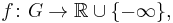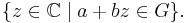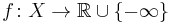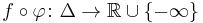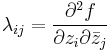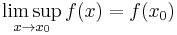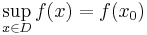Plurisubharmonic function
In mathematics, plurisubharmonic functions (sometimes abbreviated as psh, plsh, or plush functions) form an important class of functions used in complex analysis. On a Kähler manifold, plurisubharmonic functions form a subset of the subharmonic functions. However, unlike subharmonic functions (which are defined on a Riemannian manifold) plurisubharmonic functions can be defined in full generality on complex spaces.
Contents |
Formal definition
A function
with domain 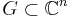 is called plurisubharmonic if it is upper semi-continuous, and for every complex line
is called plurisubharmonic if it is upper semi-continuous, and for every complex line
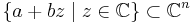 with
with 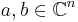
the function 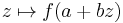 is a subharmonic function on the set
is a subharmonic function on the set
In full generality, the notion can be defined on an arbitrary complex manifold or even a complex space  as follows. An upper semi-continuous function
as follows. An upper semi-continuous function
is said to be plurisubharmonic if and only if for any holomorphic map 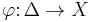 the function
the function
is subharmonic, where 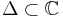 denotes the unit disk.
denotes the unit disk.
Differentiable plurisubharmonic functions
If  is of (differentiability) class
is of (differentiability) class 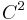 , then
, then  is plurisubharmonic, if and only if the hermitian matrix
is plurisubharmonic, if and only if the hermitian matrix 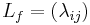 , called Levi matrix, with entries
, called Levi matrix, with entries
is positive semidefinite.
Equivalently, a 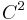 -function f is plurisubharmonic if and only if
-function f is plurisubharmonic if and only if 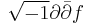 is a positive (1,1)-form.
is a positive (1,1)-form.
History
Plurisubharmonic functions were defined in 1942 by Kiyoshi Oka [1] and Pierre Lelong. [2]
Properties
- The set of plurisubharmonic functions form a convex cone in the vector space of semicontinuous functions, i.e.
-
- if
 is a plurisubharmonic function and
is a plurisubharmonic function and 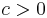 a positive real number, then the function
a positive real number, then the function 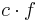 is plurisubharmonic,
is plurisubharmonic, - if
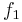 and
and 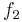 are plurisubharmonic functions, then the sum
are plurisubharmonic functions, then the sum 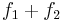 is a plurisubharmonic function.
is a plurisubharmonic function.
- if
- Plurisubharmonicity is a local property, i.e. a function is plurisubharmonic if and only if it is plurisubharmonic in a neighborhood of each point.
- If
 is plurisubharmonic and
is plurisubharmonic and 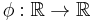 a monotonically increasing, convex function then
a monotonically increasing, convex function then 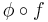 is plurisubharmonic.
is plurisubharmonic. - If
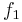 and
and 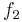 are plurisubharmonic functions, then the function
are plurisubharmonic functions, then the function 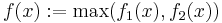 is plurisubharmonic.
is plurisubharmonic. - If
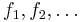 is a monotonically decreasing sequence of plurisubharmonic functions
is a monotonically decreasing sequence of plurisubharmonic functions
then so is 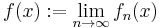 .
.
- Every continuous plurisubharmonic function can be obtained as a limit of monotonically decreasing sequence of smooth plurisubharmonic functions. Moreover, this sequence can be chosen uniformly convergent.[3]
- The inequality in the usual semi-continuity condition holds as equality, i.e. if
 is plurisubharmonic then
is plurisubharmonic then
(see limit superior and limit inferior for the definition of lim sup).
- Plurisubharmonic functions are subharmonic, for any Kähler metric.
- Therefore, plurisubharmonic functions satisfy the maximum principle, i.e. if
 is plurisubharmonic on the connected domain
is plurisubharmonic on the connected domain  and
and
for some point 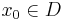 then
then  is constant.
is constant.
Applications
In complex analysis, plurisubharmonic functions are used to describe pseudoconvex domains, domains of holomorphy and Stein manifolds.
Oka theorem
The main geometric application of the theory of plurisubharmonic functions is the famous theorem proven by Kiyoshi Oka in 1942. [1]
A continuous function 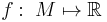 is called exhaustive if the preimage
is called exhaustive if the preimage ![f^{-1}(]-\infty, c])](/2012-wikipedia_en_all_nopic_01_2012/I/88e4cb723d513508bbbb96d0e30f3bec.png) is compact for all
is compact for all 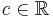 . A plurisubharmonic function f is called strongly plurisubharmonic if the form
. A plurisubharmonic function f is called strongly plurisubharmonic if the form 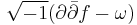 is positive, for some Kähler form
is positive, for some Kähler form  on M.
on M.
Theorem of Oka: Let M be a complex manifold, admitting a smooth, exhaustive, strongly plurisubharmonic function. Then M is Stein. Conversely, any Stein manifold admits such a function.
References
- Steven G. Krantz. Function Theory of Several Complex Variables, AMS Chelsea Publishing, Providence, Rhode Island, 1992.
- Robert C. Gunning. Introduction to Holomorphic Functions in Several Variables, Wadsworth & Brooks/Cole.
Notes
- ^ a b K. Oka, Domaines pseudoconvexes, Tohoku Math. J. 49 (1942), 15–52.
- ^ P. Lelong, Definition des fonctions plurisousharmoniques, C. R. Acd. Sci. Paris 215 (1942), 398–400.
- ^ R. E. Greene and H. Wu,
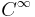 -approximations of convex, subharmonic, and plurisubharmonic functions, Ann. Scient. Ec. Norm. Sup. 12 (1979), 47–84.
-approximations of convex, subharmonic, and plurisubharmonic functions, Ann. Scient. Ec. Norm. Sup. 12 (1979), 47–84.